10869. Building construction

 

Given n buildings of height h1, h2, …, hn, the objective is to make every building has equal height. This can be done by removing bricks from a building or adding some bricks to a building. Removing a brick or adding a brick is done at certain cost which will be given along with the heights of the buildings. Find the minimal cost at which you can make the buildings look beautiful by reconstructing the buildings such that the n buildings satisfy h1 = h2 = ... = hn​ = k (k can be any non-negative integer).

For convenience, all buildings are considered to be vertical piles of bricks, which are of same dimensions.

 

Input. The first line contains number of buildings n (n ≤ 105). The second line contains n integers which denotes the heights of the buildings h1, h2, …, hn (0 ≤ hi ≤ 104). The third line contains n integers c1, c2, ..., cn (0 ≤ ci ≤ 104) which denotes the cost of adding or removing one unit of brick from the corresponding building.

 

Output. Print the minimal cost to make all the buildings look beautiful.

 

Sample input 1

Sample output 1

4

2 3 1 4

10 20 30 40

110

 

 

Sample input 2

Sample output 2

3

1 2 3

10 100 1000

120

 

 

SOLUTION

ternary search

 

Algorithm analysis

Sort the buildings by height so that h1 ≤ h2 ≤ …≤ hn​. Buildings with the same heights are sorted by increasing cost of adding / removing.

Find the cost for which we can make the height of all houses equal to hx (1 ≤ x ≤ n). It is equal

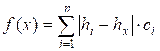
The function f(x) is concave and has a global minimum, that can be found with a ternary search.

 

Example

Consider the first example. Sort buildings by height:

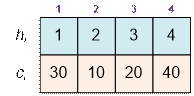
Find the value of the function f(x) for all heights:

·        f(1) = (1 – 1) * 30 + (2 – 1) * 10 + (3 – 1) * 20 + (4 – 1) * 40 = 170,

·        f(2) = (2 – 1) * 30 + (2 – 2) * 10 + (3 – 2) * 20 + (4 – 2) * 40 = 130,

·        f(3) = (3 – 1) * 30 + (3 – 2) * 10 + (3 – 3) * 20 + (4 – 3) * 40 = 110,

·        f(4) = (4 – 1) * 30 + (4 – 2) * 10 + (4 – 3) * 20 + (4 – 4) * 40 = 130

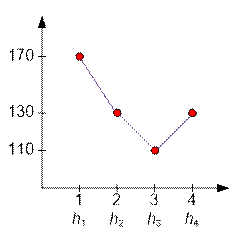
The minimum of the function f(x) is achieved at x = 3, while f(3) = 110.

 

Algorithm realization

Each building has a height h and the cost cost of adding/removing a floor. Information about buildings is stored in array b.

 

#define MAX 100001

struct Building

{

  int h, cost;

};

Building b[MAX];

 

The function cmp is a comparator for sorting buildings. Buildings are sorted by increasing height. If the heights of the buildings are the same, then sort them by increasing cost.

 

int cmp(Building a, Building b)

{

  if (a.h == b.h)

    return a.cost < b.cost;

  return a.h < b.h;

}

 

The function f calculates the cost to make all buildings equal to the height of the building number x.

 

long long f(int x)

{

  long long ret = 0;

  for (int i = 1; i <= n; i++)

    ret += 1LL * abs(b[x].h - b[i].h) * b[i].cost;

  return ret;

}

 

Function ternary_search use a ternary search to find such value of x ∈ [left; right], for which f(x) is minimum. Initially [left; right] = [1; n].

 

long long ternarySearch(int left, int right)

{

  while (right - left >= 3)

  {

    int a = left + (right - left) / 3;

    int b = left + 2 * (right - left) / 3;

    if (f(a) > f(b))

      left = a;

    else

     right = b;

  }

 

Difference between left and right no more than 3. Find the minimum of f(x) on the interval [left; right] by exhaustive search.

 

  long long res = f(left++);

  while (left <= right)

    res = min(res, f(left++));

  return res;

}

 

The main part of the program. Read the input data.

 

scanf("%d", &n);

for (i = 1; i <= n; i++)

  scanf("%d", &b[i].h);

for (i = 1; i <= n; i++)

  scanf("%d", &b[i].cost);

 

Sort the buildings.

 

sort(b + 1, b + n + 1, cmp);

 

Find and print the answer. Buildings are numbered from 1 to n.

 

printf("%lld\n", ternarySearch(1, n));